Александер
Игровая стратегия, рассматриваемая в данной статье, основана на 3 математических прогрессиях, которые применяются в разных игровых ситуациях. Вид прогрессий:
№1: 1, 3, 5, 7, 9, 11, 13, 15 …
№2: 1, 4, 7, 10, 13, 16, 19, 21 …
№3: 1, 5, 9, 13, 17, 20, 23 …
Для всех этих математических прогрессий в системе игры «Александер» предусмотрены разные индивидуальные параметры:
• номинал ставки конкретного пользователя системы;
• ступени изменения номинала ставок (ступень – это разность двух соседних чисел, которые находятся в используемой на данный момент математической прогрессии).
К примеру, уровень ступени для математической прогрессии под номером 1 равен 2, для второй – 3, а для третьей – 4.
При использовании системы «Александер» применение одной из этих математических прогрессий начинается с первой своей ставки. Дальнейшие действия зависят от исхода первой ставки игрока.
• Если ставка принесла пользователю системы поражение и его номинал равняется следующему числу в применяемой математической прогрессии, то игрок должен перейти на следующую ступень математической прогрессии.
• Если при таком переходе игрок использовал первую математическую прогрессию, то на следующую ступень переходит после 2 неудачных ставок.
• Если при переходе игрок пользуется второй математической прогрессией, тогда переход на следующую ступень осуществляется после 3 неудачных ставок.
• Если при переходе пользователь применяет третью математическую прогрессию, то на следующую ступень он передвинется после 4 неудачных ставок.
• В случае победы ставки пользователь системы переходит на предыдущую ступень математической прогрессии после достижения количества совершенных игроком ставок уровня, равного ступени в используемой математической прогрессии.
Переходы на предыдущий уровень прогрессии осуществляются так:
• Первая прогрессия: выиграв две ставки.
• Вторая прогрессия: выиграв три ставки.
• Третья прогрессия: выиграв четыре ставки.
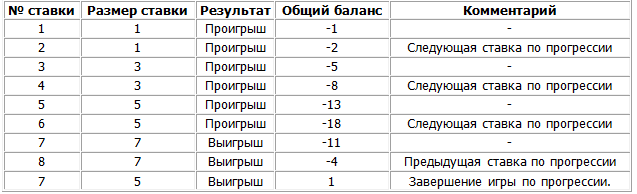
Применяйте игровую систему «Александер» до тех пор, пока не достигните положительного денежного баланса. В таблице 1 представлен пример использования математической прогрессии №1.
