Теория игр

Теория игр (на английском звучит как Theory of Games) – математический метод изучения возможных оптимальных стратегий игр, в которых участвует как минимум две стороны, ведущие борьбу за реализацию своих интересов и целей. Для этого анализируются ожидаемые стратегии и поведение других сторон, затем выбирается и используется оптимальная стратегия. Проще говоря, это математический метод выбора оптимальной стратегии, где учитывается информация и предположения о возможных ресурсах, возможных стратегий и моделях поведения всех участников игры. В современном виде теория игр включает принцип равновесия Нэша, согласно которому главная задача каждого участника игры – выбрать стратегию, которая даст результат, выгодный как себе, так и остальным сторонам игры.

Понятие о теории игр впервые появилось в 1944 году в публикации «Теория игр и экономического поведения», автора: Оскар Моргенштерн и Джон фон Нейман. В наше время теория игр распространена в большом количестве сфер как раздел прикладной математики. Данная теория широко применяется в экономике, социологии, политологии, этике, психологии, биологии, кибернетике и в игорной сфере.

В теории игр описан покер в экстенсивной форме представления игр. Он считается комбинированным типом не кооперативных игр с частично полной информацией и нулевой суммой.

Немного истории

Формы представления игр

Каждая игра является строго описанным математической моделью объектом. В данную математическую модель включены представления сторон-участников, набор доступных сторонам стратегических действий, которые формируют стратегии, комбинации стратегий и результаты игры. К этому должна стремиться каждая сторона.

В теории игр рассматриваются процессы, представленные в трех основных формах. Для кооперативных игр зачастую используется характеристическая форма представления, а для остальных – экстенсивная или нормальная форма.

Нормальная форма представления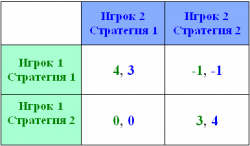

Это стратегическая форма представления процесса (игры), описываемая платежной матрицей. Каждая сторона матрицы является отдельной стороной-участником игры (игрок), где строки – стратегии одной стороны, а столбцы — это возможные стратегии второй стороны. Все значения, содержащие в матрице – это пересечение решений о выборе каждой из сторон определенной стратегии. Если игрок 1 выбирает стратегию 2, а игрок 2 выбирает стратегию 1, то оба игрока ничего не потеряют, но и ничего не приобретут (нулевое решение). Каждый игрок выбирает максимально выгодную для себя стратегию. В зависимости от поведения оппонента при выборе стратегии, это решение может оказаться не выгодным. Так представляются игры с неполной информацией.

Экстенсивная форма представления

Экстенсивная форма является расширенной формой представления игр. Для большего понятия форма изображается в форме дерева решений. Вершины – ситуации выбора одной стороны своей стратегии. В каждой стороне есть уровень вершин. После выбора каждой из сторон своего решения получается следующий результат.

Рассмотрим данный пример. Игрок 1 ходит первым, он выбирает стратегию U или F. Игрок 2 анализирует ситуацию и выбирает оптимальную стратегию, что приводит к окончательному результату.

Это наглядная форма представления, с помощью которой удобно представлять игры с двумя и более игроками, а также игры с последовательными ходами. Когда обе стороны ходят одновременно, соответствующие вершины обводятся сплошной линией или соединяются пунктиром.

Характеристическая форма представления

С помощью этой формы представляются кооперативные игры – те игры, где соревнуются не отдельные стороны, а коалиции игроков. Здесь используется характеристическая функция, с помощью которой определяется выигрыш каждой коалиции, при этом предполагается, что пустая коалиция никогда ничего не выигрывает (выигрыш равен нулю).

Эта форма основывается на нормальной форме представления. При игре с двумя сторонами получается коалиция C, ее оппонентом является коалиция N/C. Это можно сравнить с игрой двух игроков. Учитывая, что вариантов возможных коалиций множество – 2^N, где N – это количество игроков, выигрыш для C является характеристической величиной, которая зависит от состава коалиции. Игра в данной форме представляется парой (N, v), где N – все игроки, а v – это 2^N → R – характеристическая функция.
Данная форма применяется для всех игр. Это значит, что любую игру из нормальной формы можно перевести в характеристическую. В обратную сторону часто это не выполняется.

Типы игр

Кооперативные или не кооперативные игры

Кооперативной или коалиционной называют игру, в которой игроки объединяются в группы и накладывают на себя определенные обязательства перед иными участниками группы. Действия направляются на выбор тактики, которая приведет к достижению целей всей группы. Во время не кооперативной игры каждый играет «сам за себя», главная цель – достичь победы, обойдя других участников.
Не кооперативные игры описывают игру в мелких деталях, которые дает каждый участник игры (низкий уровень описания игр). Кооперативные игры описывают общую стратегию игры и поведения каждой группы. Равновесие Нэша – это решение некоторых кооперативных игр в качестве ситуации равновесия не кооперативных игр.

Игры с нулевой или ненулевой суммой

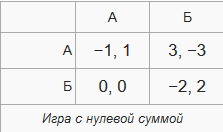
Играми с нулевой суммой называется вид игр с постоянной суммой, участники которых не в силах изменить имеющиеся ресурсы и фонд игры. В данном случае сумма всех выигрышей приравнивается к сумме проигрышей. Покер является хорошим примером такой игры, по правилам один игрок выигрывает поставленную сумму, а остальные теряют все. Можно навести жизненный пример – воровство.

Игры с ненулевой (непостоянной) суммой предполагают, что при выигрыше одного игрока не обязательно проигрывает другой, и наоборот. Исход данной игры отличается от нуля. Для преобразования игры к нулевой сумме вводится фиктивный игрок, который получает излишек или отдает недостаток средств. Пример игры с непостоянной суммой – шахматы и шашки. Жизненный пример – торговля, где выгоду извлекает каждый участник.

Игры с полной и неполной информацией

Игры с полной информацией предполагают, что участники знают все ходы, которые были сделаны до текущего момента, и стратегии противников. Благодаря этому можно предсказать дальнейшее развитие игры.
В математике игр изучаются игры с неполной информацией и частично не полной информацией. Если известны применяемые противниками стратегии, знать их ходы не необязательно.

Параллельные и последовательные игры

Во время параллельных игр все игроки ходят одновременно. Они не знают выбор своих оппонентов, пока все не походят. Обычно они показаны в нормальной форме представления.
В последовательных или динамических играх участники делают ходы в случайном или заранее установленном порядке. Есть информация о ранее выполняемых действиях других игроков. Информация может быть даже частично неполной, к примеру, игрок знает, что его противник из множества используемых стратегий не выбрал одну. Последовательные игры представлены в экстенсивной форме.

Симметричные или не симметричные игры

Во время симметричной игры соответствующие линии стратегий у игроков равны (получаются одинаковые результаты). Если два игрока поменяются местами, их шансы на выигрыш останутся такими, как и раньше. Большинство игр, особенно для двух игроков, являются симметричными.
При не симметричной игре результат применения стратегий будет разным. При выборе одной из сторон определенной стратегии результат точно будет меньшим, чем у другой стороны.

Дискретные и непрерывные игры (бесконечное число шагов)

Большинство изучаемых математикой игр дискретны. Все они имеют конечное число игроков, событий, исходов, ходов. К таким играм относятся любые процессы, происходящие в реальном мире или изучаемые в экономике. Как правило, они длятся конечное число ходов. При подборе стратегии игры учитываются временные рамки и количество итераций.
Многие игры расширены на неопределенное число ходов, поэтому продолжаются бесконечно долго. Обычно их связывают с временной шкалой. Это дифференциальные игры, хотя происходящие события часто дискретные по природе. В данном случае выбор стратегии осуществляется по-другому: делается попытка найти не оптимальное решение, а выигрышную стратегию, чтобы поддерживать положительный результат на длительной дистанции.